Zurzeit findet Schule aufgrund der Corona-Krise zu Hause statt. Die Schülerinnen und Schüler lernen vornehmlich allein mit Arbeitsblättern, Erklärungen und Übungsaufgaben. Wie kann unter diesen ungewohnten Bedingungen das Lernen möglichst gut gelingen? Prof Dr. Jörg Wittwer, Leiter der Abteilung Empirische Lehr- und Lernforschung am Institut für Erziehungswissenschaft der Albert-Ludwigs-Universität Freiburg und Mitglied des Gemeinsamen Studienauschusses der School of Education FACE, hat für interessierte Lehrer*innen Anregungen aus der empirischen Lehr-Lern-Forschung zusammengestellt, mit denen sie Schülerinnen und Schüler in ihrem Lernen allein zu Hause unterstützen können.

Unterricht in Corona-Zeiten
Zurzeit findet Schule aufgrund der Corona-Krise zu Hause statt. Vollständig ersetzt wird der herkömmliche Unterricht allerdings selten durch einen digitalen Unterricht, bei dem Schülerinnen und Schüler einer Klasse mit ihren Lehrerinnen und Lehrern über das Internet zusammenkommen. Stattdessen lernen Schülerinnen und Schüler vornehmlich allein zu Hause: Sie erhalten Arbeitsblätter, lesen Erklärungen und bearbeiten
Übungsaufgaben. Wie kann unter diesen ungewohnten Bedingungen das Lernen möglichst gut gelingen?
 Interessierte Lehrerinnen und Lehrer finden in diesem Beitrag einige Anregungen aus der empirischen Lehr-Lern-Forschung, mit denen sie Schülerinnen und Schüler in ihrem Lernen allein zu Hause unterstützen können. Die Anregungen sind aus der Literatur, die unten angegeben ist, zusammengestellt. Die Anregungen Lernziele und Motivation zeigen Möglichkeiten auf, Schülerinnen und Schülern Orientierung in dieser herausfordernden Lernsituation zu geben und ihr Interesse für neuen Lernstoff zu wecken. Zudem verdeutlichen die Anregungen Beispiele, Üben und Rückmeldung, wie man die Lernaktivitäten von Schülerinnen und Schülern so beeinflussen kann, dass sie zu einem hohen Lernerfolg führen. Die Beispiele, die in diesem Beitrag der Veranschaulichung der vorgestellten Anregungen dienen, sind bewusst einfach gehalten, damit sie für alle Lehrerinnen und Lehrer – unabhängig von ihrem Unterrichtsfach – leicht verständlich sind. Die Anregungen können natürlich genauso nützlich sein, wenn sich Schülerinnen und Schüler mit schwierigerem Lernstoff auseinandersetzen. Deshalb richten sich die Anregungen gleichermaßen an Lehrerinnen und Lehrer von Grundschulen und weiterführenden Schulen.
Interessierte Lehrerinnen und Lehrer finden in diesem Beitrag einige Anregungen aus der empirischen Lehr-Lern-Forschung, mit denen sie Schülerinnen und Schüler in ihrem Lernen allein zu Hause unterstützen können. Die Anregungen sind aus der Literatur, die unten angegeben ist, zusammengestellt. Die Anregungen Lernziele und Motivation zeigen Möglichkeiten auf, Schülerinnen und Schülern Orientierung in dieser herausfordernden Lernsituation zu geben und ihr Interesse für neuen Lernstoff zu wecken. Zudem verdeutlichen die Anregungen Beispiele, Üben und Rückmeldung, wie man die Lernaktivitäten von Schülerinnen und Schülern so beeinflussen kann, dass sie zu einem hohen Lernerfolg führen. Die Beispiele, die in diesem Beitrag der Veranschaulichung der vorgestellten Anregungen dienen, sind bewusst einfach gehalten, damit sie für alle Lehrerinnen und Lehrer – unabhängig von ihrem Unterrichtsfach – leicht verständlich sind. Die Anregungen können natürlich genauso nützlich sein, wenn sich Schülerinnen und Schüler mit schwierigerem Lernstoff auseinandersetzen. Deshalb richten sich die Anregungen gleichermaßen an Lehrerinnen und Lehrer von Grundschulen und weiterführenden Schulen.
Der Beitrag basiert auf dem Heft “Anregungen für den Unterricht in Zeiten von Corona” von Prof. Dr. Jörg Wittwer. Das Heft steht Ihnen unten zum Download zur Verfügung.
Vor dem Lernen: Lernziele und Motivation
Aufgrund der aktuellen Corona-Krise müssen Schülerinnen und Schüler zu Hause und oft allein mit Arbeitsblättern lernen. Damit ihnen klar ist, was sie beim Lernen tun sollen, ist es erforderlich, Arbeitsblätter möglichst eindeutig zu formulieren. Wichtig ist aber auch, Schülerinnen und Schülern den Nutzen des Lernens klarzumachen. Folglich sollten Lehrerinnen und Lehrer in Arbeitsblättern ihre Schülerinnen und Schüler nicht nur anweisen, was sie lernen sollen, sondern zusätzlich darüber informieren, was sie mit dem Lernen erreichen können.
Das Lernen allein zu Hause ist eine ungewohnte Situation für alle Schülerinnen und Schüler. Darunter kann ihre Bereitschaft, sich mit neuem Lernstoff zu befassen, leiden. Deshalb ist es momentan besonders wichtig, Schülerinnen und Schüler für das Lernen zu motivieren. Um dies zu tun, sollte man ihnen die Bedeutsamkeit des Lernstoffs klarmachen und sie in ihrer Erwartung, auch zu Hause erfolgreich lernen zu können, stärken.
Lernziele
Um Schülerinnen und Schüler darüber zu informieren, was sie mit dem Lernen erreichen sollen, empfiehlt es sich, Lernziele vorzugeben. Lernziele machen deutlich, was Schülerinnen und Schüler nach dem Lernen können sollen.
Beispiele für Lernziele:
Nach dem Lernen kannst du …
… die Bestandteile von Nahrung benennen.
… spitz-, recht- und stumpfwinklige Dreiecke unterscheiden.
… erklären, wann ein Gegenstand im Wasser sinkt.
… ein Lineal zum Messen von Längen benutzen.
Sowohl für Schülerinnen und Schüler als auch für Lehrerinnen und Lehrer bringen Lernziele viele Vorteile mit sich.
Vorteile für Schülerinnen und Schüler
Lernziele geben vor, was man können soll. Dadurch erfahren Schülerinnen und Schüler, welche Erwartungen an sie gestellt werden. Zugleich verschiebt sich durch Lernziele der Fokus auf das Lernen: Nicht das Abarbeiten eines Arbeitsblatts, sondern die Erreichung eines Lernziels steht im Mittelpunkt des Lernens.
Lernziel: Nach dem Lernen kannst du spitz-, recht- und stumpfwinklige Dreiecke unterscheiden.
„Ah, ich muss nicht auswendig lernen, sondern verschiedene Winkel in Dreiecken erkennen und sie voneinander unterscheiden.“
Die Vorgabe von Lernzielen aktiviert bei Schülerinnen und Schülern automatisch Vorwissen. Dadurch wird der Erwerb neuen Wissens gefördert.
Lernziel: Nach dem Lernen kannst du spitz-, recht- und stumpfwinklige Dreiecke unterscheiden.
„Ah, was Dreiecke und Winkel sind, weiß ich ja schon.“
Mit dem Wissen, welches Lernziel erreicht werden soll, kann es Schülerinnen und Schülern leichter fallen, ihr eigenes Lernen zu überwachen. Sie können feststellen, inwieweit sie sich dem vorgegebenen Lernziel nähern, und gegebenenfalls ihr Lernen anpassen.
Lernziel: Nach dem Lernen kannst du spitz-, recht- und stumpfwinklige Dreiecke unterscheiden.
„Oh, ich glaube, ich verwechsle noch spitz- mit stumpfwinklig. Das muss ich mir noch einmal genauer anschauen.“
Vorteile für Lehrerinnen und Lehrer
Lernziele konkretisieren, welches Wissen Schülerinnen und Schüler erwerben müssen. Dadurch wird es für Lehrerinnen und Lehrer einfacher, eine Lernmethode auszuwählen, mit der Schülerinnen und Schüler optimal das Wissen erwerben, das für die Erreichung eines Lernziels notwendig ist.
Beispiel: Schülerinnen und Schüler sollen Wissen über die Konzepte spitzwinklig, rechtwinklig und stumpfwinklig in Dreiecken erwerben. Eine geeignete Methode ist der Fallvergleich, bei der Dreiecke miteinander verglichen werden, indem Gemeinsamkeiten und Unterschiede gesucht werden.
Auf der Grundlage von Lernzielen können Lehrerinnen und Lehrer Vorwissens-, Übungs- und Testaufgaben erstellen. Vorwissensaufgaben erfassen das Wissen, das bereits vorhanden sein sollte, damit man mit der neuen Lerneinheit beginnen kann. Übungsaufgaben sind Teil der Lernphase und helfen Schülerinnen und Schülern, ihr neues Wissen anzuwenden. Mit Testaufgaben kann nach dem Lernen festgestellt werden, inwieweit Schülerinnen und Schüler die Lernziele erreicht haben.
Beispiele:
Vorwissensaufgabe: Zeichne ein Dreieck.
Übungsaufgabe: Zeichne ein rechtwinkliges Dreieck.
Testaufgabe: Markiere alle spitzwinkligen Dreiecke.
Lehrerinnen und Lehrer können sich bei der Rückmeldung über den Leistungsstand von Schülerinnen und Schülern direkt auf Lernziele beziehen. So können sie Schülerinnen und Schüler konkret auf ihre individuellen Stärken und Schwächen hinweisen.
Beispiel: „Du kannst rechtwinklige Dreiecke sicher erkennen. Bei der Unterscheidung zwischen spitz- und stumpfwinkligen Dreiecken machst du noch manchmal Fehler.“
Schritte bei der Erstellung von Lernzielen
Damit Lernziele das Lernen von Schülerinnen und Schülern optimal unterstützen, sind folgende Schritte bei der Erstellung von Lernzielen zu beachten:
Legen Sie fest, was Ihre Schülerinnen und Schüler nach einer Lerneinheit können sollen. Hierzu empfiehlt es sich, zu überlegen, welche Art von Wissen Schülerinnen und Schüler anwenden müssen, um ein Lernziel zu erreichen. Man unterscheidet üblicherweise vier Arten von Wissen: Fakten, Konzepte, Prinzipien und Prozeduren.
- Fakten: Das Lernziel erfordert, dass Schülerinnen und Schüler etwas erinnern (z.B. Jahr des Mauerfalls) oder wiedergeben (z.B. ein Gedicht).
- Konzepte: Das Lernziel gibt vor, dass Schülerinnen und Schüler etwas erkennen (z.B. Verb im Satz identifizieren) oder ein Beispiel für etwas geben (z.B. Rechteck zeichnen). Konzepte werden auch als Begriffe oder Kategorien bezeichnet.
- Prinzipien: Um das Lernziel zu erreichen, müssen Schülerinnen und Schüler etwas erklären (z.B. warum ein s bei he plays) oder etwas vorhersagen (z.B. was mit einem Ballon passiert, wenn Luft erhitzt wird). Hierzu müssen sie Konzepte in Beziehung zueinander setzen. Prinzipien können beispielsweise Regeln, Gesetze oder Axiome sein.
- Prozeduren: Das Lernziel verlangt von Schülerinnen und Schülern, dass sie Schritte ausführen, um ein Ziel zu erreichen (z.B. Rechenaufgabe lösen). Die Schritte können direkt beobachtbar sein (z.B. mikroskopieren) oder nur im Kopf stattfinden (z.B. Zahlen addieren). Häufig wird bei einer Prozedur nach einem bestimmten Prinzip vorgegangen. Man kann beispielsweise ein Komma in einem Satz bloß nach Gefühl oder entsprechend den Kommaregeln setzen.
Wie die Darstellung zeigt, stehen Wissensarten oft in einer direkten Beziehung zueinander. Sollen Schülerinnen und Schüler beispielsweise die Länge der Hypotenuse in einem rechtwinkligen Dreieck bestimmen (Prozedur), benötigen sie Wissen über den Satz des Pythagoras (Prinzip) und über die Eigenschaften von Dreiecken wie ihre Rechtwinkligkeit (Konzept). Bei der Regel he, she, it – das s muss mit (Prinzip) ist Wissen über Konzepte wie Verb, Infinitivform und simple present nötig.
Damit Schülerinnen und Schülern klar ist, welche Anforderungen sie erfüllen sollen, ist es wichtig, Lernziele so eindeutig wie möglich zu formulieren. Um dies zu erreichen, sollten Sie in Lernzielen nur solche Verben verwenden, die direkt beobachtbare Tätigkeiten beschreiben.
- Lernziele zu Fakten: Das Erinnern von Informationen ist beobachtbar, wenn Schülerinnen und Schüler etwas nennen, beschreiben oder auflisten.
Beispiel: Du kannst die Definition von spitzwinklig nennen. - Lernziele zu Konzepten: Das Erkennen, dass Dinge zu einem Konzept gehören, kann man beobachten, wenn Schülerinnen und Schüler diese Dinge in einer bestimmten Weise kenntlich machen (z.B. farbig markieren).
Beispiel: Du kannst alle vorgegebenen Nebensätze, die ein Temporalsatz sind, markieren.
Das Erkennen zeigt sich auch darin, dass Schülerinnen und Schüler ein eigenes Beispiel geben können, indem sie etwas zeichnen oder aufschreiben.
Beispiel: Du kannst ein spitzwinkliges Dreieck zeichnen. - Lernziele zu Prinzipien: Das Erklären oder das Vorhersagen kann man beobachten, wenn Schülerinnen und Schüler genau dies tun.
Beispiel: Du kannst erklären, warum bei den vorgegebenen Sätzen ein s an das Verb angehängt wird. - Lernziele zu Prozeduren: Das Ausführen von Schritten (z.B. mikroskopieren) oder das Ergebnis der ausgeführten Schritte (z.B. Fläche eines Rechtecks bestimmen) ist meist direkt beobachtbar. Deshalb sind Verben zu verwenden, die unmittelbar die Prozedur ausdrücken.
Beispiel: Du kannst aus vorgegebenen Zahlen den Mittelwert berechnen.
Es empfiehlt sich, Schülerinnen und Schülern Lernziele in anregender Weise darzubieten. Beispielsweise kann man nach der Vorgabe eines Lernziels als Lehrerin oder Lehrer selbst vormachen, was Schülerinnen und Schüler nach dem Lernen können sollen (z.B. Gedicht vortragen, Geodreieck verwenden, W-Fragen beantworten). Dies ist vor allem bei Lernzielen zu Prozeduren wichtig, da diese Lernziele gewöhnlich schwierig sind. Hierzu sind kurze Videosequenzen besonders gut geeignet. Zudem kann man in Lernzielen explizit auf bereits vorhandenes Wissen Bezug nehmen. Beispielsweise kann man darstellen, dass sich die Schülerinnen und Schüler schon mit bestimmten Konzepten (z.B. Dreieck, Winkel) beschäftigt haben und es beim bevorstehenden Lernen um die Beziehung zwischen diesen Konzepten (z.B. Winkel in Dreiecken) geht. Schließlich kann man auf die Wichtigkeit von Lernzielen für die Schülerinnen und Schüler hinweisen, um deren Motivation zu fördern.
Motivation
In Zeiten von Corona kann das Lernen zu Hause unter mangelnder Motivation leiden. Schülerinnen und Schüler können sich in den eigenen vier Wänden ablenken lassen und stattdessen anderen Tätigkeiten nachgehen, die für sie interessanter als die Auseinandersetzung mit neuen Lerninhalten sind. Ohne Einbindung in eine soziale Gruppe mag das Lernen auch nicht so spannend sein und kann daher schnell als langweilig erlebt werden.
Ein hohe Motivation von Schülerinnen und Schülern ist allerdings eine unabdingbare Voraussetzung für eine aktive Auseinandersetzung mit neuen Lerninhalten. Die Bereitschaft, sich mit neuen Lerninhalten zu beschäftigen, hängt vor allem von zwei Aspekten ab. Der erste Aspekt ist die Wichtigkeit, die neue Lerninhalte für Schülerinnen und Schüler haben. Der zweite Aspekt ist die Erwartung, dass sich Schülerinnen und Schüler die neuen Lerninhalte erfolgreich aneignen können.
Um Schülerinnen und Schülern die Wichtigkeit von Lerninhalten zu verdeutlichen, können Lehrerinnen und Lehrer in Arbeitsblättern direkt Bezug auf Lernziele nehmen. Es gibt verschiedene Möglichkeiten, die Wichtigkeit von Lernzielen hervorzuheben. Man kann Schülerinnen und Schülern die Bedeutung der Lernziele für ihre eigene Lebenswelt klarmachen.
Beispiel: Beim Thema Sinken und Schwimmen wird dargestellt, warum große Schiffe nicht untergehen.
Ist kein unmittelbarer Bezug zur Lebenswelt der Schülerinnen und Schüler vorhanden, empfiehlt es sich, Situationen zu präsentieren, für deren erfolgreiche Bewältigung die Aneignung der neuen Lerninhalte notwendig ist.
Beispiel: Beim Thema Winkel in Dreiecken wird eine spannende Geschichte vorgegeben, in der Schülerinnen und Schüler helfen sollen, nach spitz- und stumpfwinkligen Dreiecken zu suchen.
Geht es um das Erlernen einer Prozedur, kann man die Vorteile der Prozedur für die Bearbeitung einer Aufgabe aufzeigen.
Beispiele:
Beim Lernen des Versmaßes können Lehrerinnen und Lehrer zeigen, dass durch Klatschen ein Rhythmus erkennbar wird.
Beim Lernen des Dreisatzes können Schülerinnen und Schüler erfahren, dass sie mit dieser Methode den Preis eines Einzelstücks schnell berechnen können.
Man kann auch die Bedeutung von Lernzielen für das zukünftige Verhalten der Schülerinnen und Schüler darstellen. Dadurch können Lernziele, die an sich nicht motivierend sind, dennoch motivationsförderlich wirken.
Beispiel: Das Lernen von Englischvokabeln mag an sich nicht besonders motivierend sein. Der Hinweis, dass Schülerinnen und Schüler mit dem Erwerb der Englischvokabeln später einen Besuch in einem englischen Restaurant problemlos meistern werden, kann das Engagement, Vokabeln zu lernen, erhöhen.
Um Schülerinnen und Schüler in ihrer Erwartung zu stärken, sich die neuen Lerninhalte erfolgreich aneignen zu können, ist es ratsam, ihnen einen Überblick über das bevorstehende Lernen zu geben. Neben einer kurzen Vorstellung der Inhalte sollte vor allem das methodische Vorgehen erläutert werden. Dabei ist es wichtig, den Schülerinnen und Schülern zu verdeutlichen, dass sie mit dem methodischen Vorgehen erfolgreich lernen können. Es sollte auch betont werden, dass sie nicht sofort alles verstehen müssen und es nicht ungewöhnlich ist, wenn sie anfänglich noch Fehler begehen.
Beispiel: Nach dem Lernen kannst du spitz- und stumpfwinklige Dreiecke erkennen. Mit dieser Fähigkeit sollst du später Robin, den du in einer Geschichte kennenlernen wirst, helfen, genau solche Dreiecke zu entdecken. Ich werde erst einmal erklären, was spitz- und stumpfwinklige Dreiecke sind. Dann werde ich dir einige spitz- und stumpfwinklige Dreiecke zeigen und auch darstellen, wie sich diese Dreiecke von anderen Dreiecken unterscheiden. Anschließend bist du an der Reihe: Du musst nicht sofort wissen, was spitz- und stumpfwinklige Dreiecke sind. Du sollst erst einmal üben, indem du Dreiecke, die ich dir vorgebe, miteinander vergleichst. Dabei kann es auch passieren, dass du noch Fehler machst. Mit diesem Vorgehen kannst du später spitz- und stumpfwinklige Dreiecke sicher erkennen und Robin helfen.
Während des Lernens: Beispiele, Üben und Rückmeldung
Gegenwärtig erhalten Schülerinnen und Schüler oft die Anweisung, eine Erklärung zu einem Lerninhalt zu lesen oder sich in einem Video anzuschauen. Der Lerninhalt wird in der Erklärung gewöhnlich anhand eines Beispiels verdeutlicht. Anschließend sollen Schülerinnen und Schüler eigenständig Aufgaben bearbeiten. In dieser Lernsituation können sie allerdings nicht wie gewohnt ihren Lehrerinnen und Lehrern sofort Fragen stellen, um Verständnisschwierigkeiten zu beseitigen. Deshalb ist es beim Lernen zu Hause besonders wichtig, dass Schülerinnen und Schüler nicht nur verständliche Erklärungen erhalten, sondern auch viele Beispiele zur Veranschaulichung der neuen Lerninhalte studieren und ihr neu erworbenes Wissen durch Übungsaufgaben festigen können.
Viele Beispiele
Damit Schülerinnen und Schüler aus Erklärungen erfolgreich lernen, reicht es gewöhnlich nicht aus, nur ein Beispiel zu geben. Stattdessen ist es häufig lernförderlicher, weitere Beispiele zu zeigen, die Schülerinnen und Schüler aktiv verarbeiten.
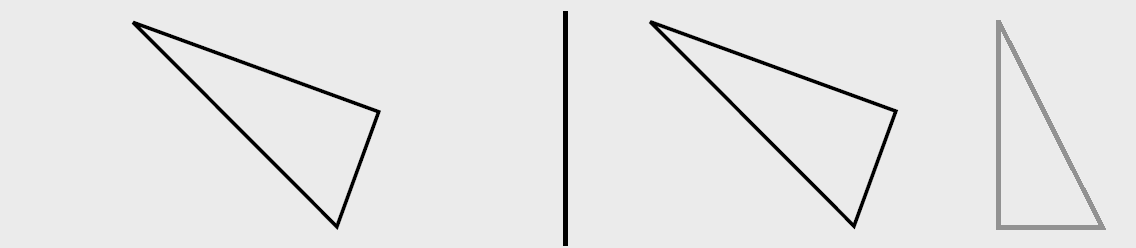
Warum ist das so? Sie sehen links eine geometrische Figur. Sie erkennen sofort, dass es ein Dreieck ist. Rechts sehen Sie zwei geometrische Figuren. Auch hierbei handelt es sich jeweils um ein Dreieck. Bei den zwei Dreiecken wird aber zusätzlich eine Gemeinsamkeit direkt erkennbar: Beide haben einen rechten Winkel.
Wenn Schülerinnen und Schüler lernen, was ein rechtwinkliges Dreieck ist, helfen mehrere Beispiele, die wesentliche Eigenschaft dieser Art von Dreiecken, das Vorhandensein eines rechten Winkels, zu erkennen. Wird hingegen nur ein Beispiel gezeigt, ist Schülerinnen und Schülern nicht unbedingt klar, worauf sie im Dreieck achten sollen, und zwar auch dann, wenn sie vorher eine Erklärung erhalten haben.
Somit liegt der Vorteil mehrerer Beispiele darin, dass Schülerinnen und Schüler diese miteinander vergleichen können. Sie können wichtige Gemeinsamkeiten zwischen den Beispielen erkennen. Zugleich erfahren sie, dass es Unterschiede zwischen den Beispielen gibt, die für das Verstehen nicht bedeutsam sind. Das Vergleichen trägt zum Aufbau eines generalisierten, d.h. vom jeweiligen Beispiel losgelösten, Wissens bei.
Viele Beispiele führen allerdings nicht automatisch zu viel Lernen. Um das Potenzial von Beispielen auszuschöpfen, ist es wichtig, gezielt Lernprozesse bei Schülerinnen und Schülern anzustoßen. Dies kann durch Aufforderungen in Form sogenannter Prompts erfolgen. Abhängig davon, ob Schülerinnen und Schüler Konzepte, Prinzipien oder Prozeduren lernen, sehen die Erklärungen und Prompts jeweils unterschiedlich aus1.
1Beispiele für Fakten gibt es nicht, weil Fakten selbst Beispiele sind (Die Glocke ist ein Beispiel für ein Gedicht, das man auswendig lernen kann).
Eine Erklärung zu einem Konzept besteht typischerweise in einer Definition und Beispielen. Konkrete Konzepte sind gewöhnlich einfacher zu erlernen als abstrakte Konzepte.
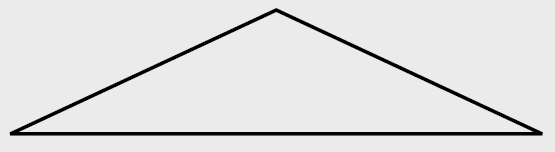
![]() Beispiel für konkretes Konzept: Ein rechtwinkliges Dreieck ist ein Dreieck mit einem rechten Winkel.
Beispiel für konkretes Konzept: Ein rechtwinkliges Dreieck ist ein Dreieck mit einem rechten Winkel.
Beispiel für abstraktes Konzept: Eine Primzahl ist eine Zahl, die nur durch 1 und sich selbst teilbar ist.
3 7 11 13 17 19 53 61 97
Dies liegt daran, dass man die wesentlichen Merkmale bei konkreten Konzepten direkt wahrnehmen kann, was bei abstrakten Konzepten nicht der Fall ist.
Um die Lernprozesse von Schülerinnen und Schülern bei der Verarbeitung von Beispielen für Konzepte günstig zu beeinflussen, empfehlen sich folgende Prompts:
- Fordern Sie Schülerinnen und Schüler zu einem Vergleich der vorgegebenen Beispiele auf (z.B. Suche nach Gemeinsamkeiten und Unterschieden zwischen den Dreiecken!). Ist zu erwarten, dass diese allgemeine Aufforderung nicht erfolgversprechend ist, sollte die Aufforderung spezifischer sein (z.B. Suche nach Gemeinsamkeiten und Unterschieden bei den Winkeln zwischen den Dreiecken!).
- Fordern Sie Schülerinnen und Schüler auf, in den vorgegebenen Beispielen nach den wesentlichen Merkmalen eines Konzepts zu suchen (z.B. Wo ist der rechte Winkel im Dreieck?). Eine spezifischere Variante ist es, das wesentliche Merkmal in einem Beispiel zu zeigen und es im anderen Beispiel suchen zu lassen (Du siehst den rechten Winkel links im Dreieck. Wo ist er im Dreieck rechts?).
- Fordern Sie Schülerinnen und Schüler nicht zu früh auf, sich selbst Beispiele für ein Konzept auszudenken. In dieser Phase des Lernens sind sie gewöhnlich mit der eigenständigen Entwicklung von Beispielen noch überfordert.
Kann ein Konzept (z.B. stumpfwinklig) mit einem anderen Konzept (z.B. spitzwinklig) verwechselt werden, empfiehlt es sich, Beispiele für das Konzept zusammen mit Beispielen für das andere Konzept zu zeigen. Dadurch wird klarer, was das zu erlernende Konzept vom anderen Konzept unterscheidet.
Bei einer Erklärung zu einem Prinzip wird häufig das Prinzip in Form einer Regel genannt. Dann werden beispielhaft Situationen vorgestellt, in denen das Prinzip anwendbar ist.
Beispiel: Wenn ein Satz in der dritten Person (he, she, it) steht, wird an die Infinitivform des Verbs ein s angehängt.
He plays piano.
She wears a hat.
It costs a lot.
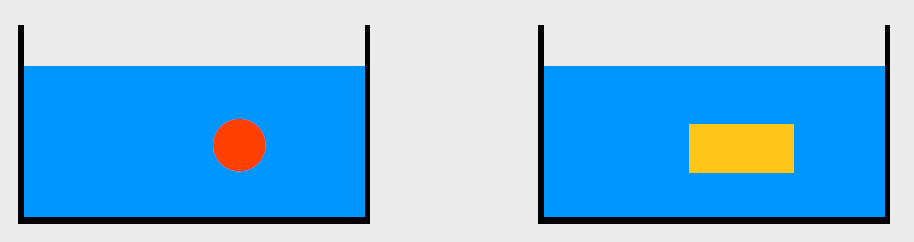 Beispiel: Wenn die Dichte eines Körpers größer als die Dichte von Wasser ist, sinkt der Körper.
Beispiel: Wenn die Dichte eines Körpers größer als die Dichte von Wasser ist, sinkt der Körper.
Zur Unterstützung des Lernens mit Beispielen für Prinzipien sind folgende Prompts geeignet:
- Fordern Sie Schülerinnen und Schüler zu einem Vergleich der vorgegebenen Beispiele auf (z.B. Suche nach Gemeinsamkeiten und Unterschieden zwischen den Sätzen!). Die Aufforderung kann auch spezifisch erfolgen (z.B. Suche nach Gemeinsamkeiten und Unterschieden bei den Verben zwischen den Sätzen!).
- Fordern Sie Schülerinnen und Schüler auf, das Ergebnis des angewendeten Prinzips in den vorgegebenen Beispielen zu suchen (z.B. Wo ändert sich etwas im Satz?).
- Fordern Sie Schülerinnen und Schüler auf, nach den Bedingungen zu suchen, unter denen das Prinzip angewendet wird, um die Anwendungsbreite des Prinzips zu verdeutlichen (z.B. Warum wird hier die Regel ‚he, she, it – das s muss mit‘ angewendet?). Man kann auch zeigen, warum das Prinzip in einem Beispiel angewendet wird, und Schülerinnen und Schüler für das andere Beispiel die Anwendungsbedingungen erklären lassen.
Oft wird eine Prozedur durchgeführt, indem das zugrunde liegende Prinzip angewendet wird. Deshalb besteht eine Erklärung zu einer Prozedur gewöhnlich in der Darstellung des Prinzips. Anschließend wird anhand von Aufgaben, die für die Schülerinnen und Schüler bereits gelöst sind, gezeigt, wie die Prozedur durchzuführen ist. Diese Lösungsbeispiele bestehen aus einzelnen Lösungsschritten und der Lösung.
Beispiel: Für ein rechtwinkliges Dreieck gilt: a2 + b2 = c2.
Du baust eine Rampe. Das Brett waagerecht auf dem Boden ist 4 m lang, das Brett senkrecht zu dem Boden ist 3 m lang. Wie lang ist das Brett für die Rampe?
Das eine Brett ist 4 m lang. Das andere Brett ist 3 m lang.
42 m2 + 32 m2 = 25 m2
√25 m2 = 5 m
Das Brett für die Rampe ist 5 m lang.
Du lehnst eine Leiter an ein Haus. Die Hauswand ist 10 m hoch. Unten auf dem ebenen Boden ist die Leiter von der Hauswand 2 m entfernt. Wie lang ist die Leiter?
Die Hauswand ist 10 m hoch. Der Boden ist 2 m lang.
102 m2 + 22 m2 = 104 m2
√104 m2 = 10.20 m
Die Länge der Leiter beträgt 10.20 m.
Lernprozesse zur Verarbeitung von Lösungsbeispielen zu Prozeduren können durch folgende Prompts angeregt werden:
- Fordern Sie Schülerinnen und Schüler auf, die einzelnen Lösungsschritte in einem vorgegebenen Lösungsbeispiel sich selbst zu erklären. Dabei sollten die Lösungsschritte auf das zugrundeliegende Prinzip bezogen werden (z.B. Warum wird dieser Lösungsschritt gemacht? Welches Prinzip wird hier angewendet?). Es ist auch möglich, die Aufforderung direkt auf das zugrunde liegende Prinzip zu beziehen (z.B. Warum wird bei diesem Lösungsschritt addiert?).
- Fordern Sie Schülerinnen und Schüler auf, die vorgegebenen Lösungsbeispiele miteinander zu vergleichen. (z.B. Suche nach Gemeinsamkeiten und Unterschieden zwischen den Aufgaben!). Die Aufforderung kann auch spezifischer in Bezug auf einzelne Lösungsschritte erfolgen (z.B. Suche nach Gemeinsamkeiten und Unterschieden beim Addieren zwischen den Aufgaben!).
Damit Schülerinnen und Schüler generalisiertes Wissen aufbauen, sollten Sie Lösungsbeispiele mit unterschiedlichen Oberflächenmerkmalen vorgeben. Die zwei Lösungsbeispiele im Kasten weisen beispielsweise dasselbe Prinzip (Satz des Pythagoras), aber unterschiedliche Oberflächenmerkmale auf (Rampe, Leiter). Dadurch können Schülerinnen und Schüler lernen, dass Oberflächenmerkmale für die Durchführung einer Prozedur an sich nicht relevant sind. So erwerben sie Wissen, das vom konkreten Lösungsbeispiel losgelöst ist.
Geben Sie ausreichend viele Lösungsbeispiele vor und lassen Sie die Schülerinnen und Schüler nicht sofort Aufgaben selbst lösen. Dies ist wichtig, weil Schülerinnen und Schüler in der anfänglichen Lernphase noch kein generalisiertes Wissen besitzen, mit dem sie die Prozedur direkt auf unterschiedliche Aufgaben flexibel anwenden könnten. Dagegen dient gerade die Auseinandersetzung mit Lösungsbeispielen dem Aufbau eines solchen Wissens.
Üben
Nachdem Schülerinnen und Schüler Erklärungen und Beispiele verarbeitet haben, ist es notwendig, dass sie ihr neu erworbenes Wissen festigen können. Deshalb sollte die Lernphase auch Übungsaufgaben enthalten. Dabei ist es wichtig, dass die Übungsaufgaben die gesamte Komplexität der zu erwerbenden Lerninhalte abdecken.
Schülerinnen und Schülern sollte klar gemacht werden, dass die Bearbeitung der Übungsaufgaben dem Lernen dienen. Deshalb müssen die Schülerinnen und Schüler die Übungsaufgaben nicht fehlerfrei bearbeiten. Je nach Lernziel sind die Übungsaufgaben unterschiedlich zu erstellen.
Die Aufgaben erfordern, etwas wiederzugeben. Es sollte klar sein, ob dies wörtlich geschehen soll.
Gib die Definition von spitzwinklig in eigenen Worten wieder.
In den Aufgaben müssen Beispiele zu einem Konzept erkannt oder selbst Beispiele gegeben werden. Gelegentlich sollte das Konzept erklärt werden.
Erkennen: Markiere alle rechtwinkligen Dreiecke.
Geben: Zeichne ein rechtwinkliges Dreieck.
Erklären: Warum ist das ein rechtwinkliges Dreieck?
Bei den Aufgaben muss man etwas erklären oder vorhersagen. Zusätzlich können Aufgaben nur nach den Anwendungsbedingungen eines Prinzips fragen.
Erklären: Warum schwimmt Olivenöl auf Wasser?
Vorhersagen: Was passiert, wenn sich ein Mensch im Wasser nicht bewegt?
Anwendungsbedingungen: Ein Körper hat eine Dichte von 1,1 g / cm3. In welcher Flüssigkeit sinkt der Körper? Warum?
Wasser Methanol Glycerin
Die Aufgaben erfordern, dass Schülerinnen und Schüler die Schritte einer Prozedur durchführen. Man kann auch einige Schritte vorgeben und um die Bearbeitung der weiteren Schritte bitten. Zudem kann man Schülerinnen und Schüler nur nach den Anwendungsbedingungen einer Prozedur fragen.
Alle Schritte durchführen:
Du hast ein Rechteck mit einer Länge von 4 cm und einer Breite von 2 cm.
Wie lang ist die Diagonale?
Weitere Schritte durchführen:
Du hast ein Quadrat mit einer Seitenlänge von 3 cm.
Wie lang ist die Diagonale? Der erste Schritt ist bereits für dich gelöst: 32 cm2
Führe alle weiteren Schritte durch.
Anwendungsbedingungen:
Kannst du hier die Länge der längsten Seite im Dreieck mit dem Satz des Pythagoras bestimmen? Warum (nicht)?
Rückmeldung
Besonders beim Lernen zu Hause kann es motivierend sein, wenn Schülerinnen und Schüler Rückmeldung zu den bearbeiteten Übungsaufgaben erhalten. Durch eine Rückmeldung können sie auch Verständnisprobleme und Wissenslücken beseitigen. Ist eine individuelle Rückmeldung nicht möglich, sollten Schülerinnen und Schüler ihre Bearbeitung der Übungsaufgaben mit der richtigen Lösung vergleichen können. Damit sie bei diesem Vergleich erkennen, warum sie etwas falsch gemacht haben, sollte man sie mit Fragen gezielt unterstützen. Die richtigen Lösungen und Fragen zum Vergleichen können Sie Schülerinnen und Schülern bereitstellen.
Eine Aufgabe kann beispielsweise falsch sein, weil Informationen nicht wortwörtlich oder in falscher Reihenfolge wiedergegeben werden.
Beispiele:
Hast du die Definition auch wortwörtlich wiedergegeben?
Hast du die Sätze in der richtigen Reihenfolge genannt?
Eine Aufgabe kann beispielsweise falsch sein, weil ein Beispiel für ein Konzept nicht als solches erkannt wird. Oder es wird bei einem Beispiel ein Konzept erkannt, das auf das Beispiel nicht zutrifft. Es ist auch möglich, nach den wesentlichen Merkmalen eines Konzepts zu fragen.
Beispiele:
Hast du ein Dreieck als spitzwinkliges Dreieck markiert, obwohl es keins ist?
Hast du ein Dreieck nicht als spitzwinkliges Dreieck markiert, obwohl es eins ist?
Ist dir klar, was das wesentliche Merkmal eines spitzwinkligen Dreiecks ist?
Eine Aufgabe kann beispielsweise falsch sein, weil das Prinzip nicht erinnert, die Situation, in der das Prinzip anwendbar ist, nicht erkannt oder das Prinzip falsch angewendet wird.
Beispiele:
Kannst du den Satz des Pythagoras richtig nennen?
Ist in dem Satz kein s an das Verb angehängt, weil der Satz nicht im simple present steht?
Hast du die Dichte und nicht das Gewicht beachtet, um vorherzusagen, ob der Körper im Wasser sinkt?
Eine Aufgabe kann beispielsweise falsch sein, weil die Schritte zur Durchführung der Prozedur nicht erinnert werden, die Situation, in der die Prozedur anwendbar ist, nicht erkannt wird oder die Schritte falsch durchgeführt werden.
Beispiele:
Kannst du alle Schritte zur Bestimmung der Länge der Hypotenuse nennen?
Handelt es sich um ein rechtwinkliges Dreieck?
Hast du bei dem entsprechenden Schritt quadriert?
Schlussbemerkung
Ich hoffe, dass Sie einige der Anregungen hilfreich finden und nutzen können, um das Lernen Ihrer Schülerinnen und Schüler zu Hause zu unterstützen. Die Anregungen können selbstverständlich nicht nur für das Unterrichten in Corona-Zeiten nützlich sein, sondern auch allgemein bei der Unterrichtsplanung berücksichtigt werden. Aufgrund der Corona-Krise scheinen mir die ausgewählten Anregungen aber momentan besonders wichtig für das Unterrichten, vor allem für das Unterrichten mit Arbeitsblättern, zu sein.
Jörg Wittwer ist Pädagogischer Psychologe und seit 2010 Professor für Empirische Lehr-und Lernforschung, von 2010 bis 2013 an der Universität Göttingen, seit 2013 am Institut für Erziehungswissenschaft der Universität Freiburg.
Prof. Dr. Jörg Wittwer
Institut für Erziehungswissenschaft
Universität Freiburg
joerg.wittwer@ezw.uni-freiburg.de
Literatur
Alfieri, L., Nokes-Malach, T. J. & Schunn, C. D. (2013). Learning through case comparisons: A meta-analytic review. Educational Psychologist, 48, 87–113.
Gronlund, N. E. & Brookhart, S. M. (2008). Gronlund’s writing instructional objectives. New York: Prentice Hall.
Renkl, A. (2014). Towards an instructionally-oriented theory of example-based learning. Cognitive Science, 38, 1–37.
Smith, P. L. & Ragan, T. J. (2005). Instructional design (3. Aufl.). New York: Wiley.
Wittwer, J., Kratschmayr, L. & Voss, T. (2019). Wie gut erkennen Lehrkräfte typische Fehler in der Formulierung von Lernzielen? Unterrichtswissenschaft, 48, 113–128.
Wittwer, J. & Renkl, A. (2008). Why instructional explanations often do not work: A framework for understanding the effectiveness of instructional explanations. Educational Psychologist, 43, 49–64.
Wittwer, J. & Renkl, A. (2010). How effective are instructional explanations in examplebased learning? A meta-analytic review. Educational Psychology Review, 22, 393–409.
Zamary, A. & Rawson, K. A. (2018). Are provided examples or faded examples more effective for declarative concept learning? Educational Psychology Review, 30, 1167–1197.
Weiterlesen
Einen wissenschaftlichen Artikel zu dem Thema “Unterricht in Zeiten von Corona” des Autors finden Sie hier (frei zugänglich):
https://doi.org/10.1007/s42010-020-00088-2